How To Draw Acceleration Time Graph From Velocity Time Graph
Motion graphs, too known every bit kinematic curves, are a common manner to diagram move in physics. The iii move graphs a high school physics student needs to know are:
- Position vs. time (x vs. t)
- Velocity vs. time (5 vs. t)
- Acceleration vs. time (a vs. t)
Each of these graphs helps to tell the story of the motion of an object. Moreover, when the position, velocity and dispatch of an object are graphed over the the same time interval, the shapes of each graph chronicle in a specific and predictable mode.
Setting upwards Motion Graphs
The x-axis on all motion graphs is always time, measured in seconds. The axis is thus ever labeled t(s).
The y-centrality on each graph is position in meters, labeled x(one thousand); velocity in meters per second, labeled five(m/south); or acceleration in meters per second squared, labeled a(m/s2)
Tips
-
Beware of the position axis characterization x (grand) – the "x" stands for displacement, not "ten-axis"!
Motility graphs are often (though certainly non always) sketched without graphing specific points, instead showing a full general shape that describes the relative motion of an object.
Position-Time Graphs
The position of an object can be positive or negative, depending on the frame of reference. Whatever the diagram shows, the coordinate plane must match.
Consider the example of a kid riding along a straight line e and so w on her cycle. Phone call east the positive direction and west the negative direction.
Here is a graph of her ride:
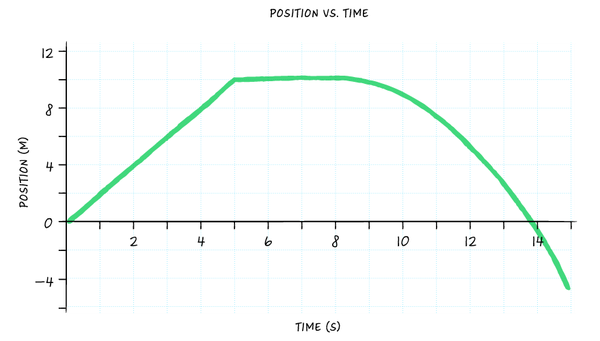
••• Dana Chen | Sciencing
For the first five seconds of her ride (from t = 0 to t = five), she was moving at a abiding rate to the east. This is indicated by the straight, increasing line in the positive quadrant of the position-time graph. Some other mode to think of it is that her position is increasing positively.
In the next three seconds (t = five to t = eight), she stopped for a break. Her position does not alter in this time period, indicated past a abiding horizontal line stuck at +10 m.
Finally, the girl on the bicycle in the concluding part of her ride (t = 8 to t = 15) begins accelerating back in the due west direction. This is indicated past a line that is non-constant (curved) and heading into the negative quadrant of the graph. The gradient of the line increases over time, in the negative direction, showing that her speed is increasing as she covers more ground every 2nd.
Note that when she crosses the x-axis, she has passed by the place where she started out.
Velocity-Time Graphs
Position-time graphs lead directly to velocity-time graphs: The slope of a position-time line shows the velocity of the object in the same time interval. This makes sense because position vs. time is merely some other way of saying meters per second – the definition of velocity.
In this example, the only difference is what goes on the y-axis.
Consider the same girl on her bike as in the terminal department. For the offset five seconds of her ride, she traveled 10 meters in five seconds, or 2 meters per 2nd.
To graph her velocity in that aforementioned fourth dimension interval and then, notice ii m/s on the y-axis and draw a flat line for the first five seconds. Call back, her velocity didn't change, and so the gradient on this graph is goose egg. (Which means graphing her acceleration in this fourth dimension interval should exist even easier – keep reading.)
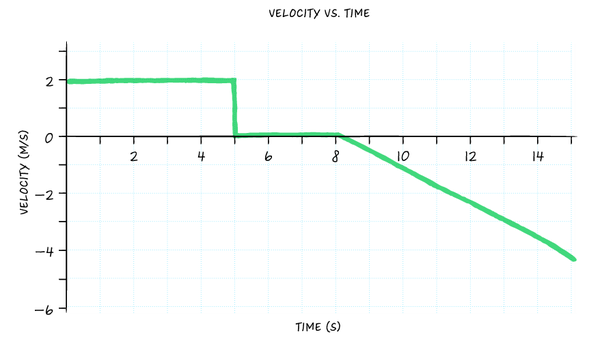
••• Dana Chen | Sciencing
Then, for the side by side three seconds, she didn't motion at all, then her velocity abruptly dropped to zero. (Realistically, yes, she must take decelerated from ii m/due south to 0 m/s in more an instant. But for the sake of simplicity hither, consider that her speed changed instantaneously.)
Of class, if her velocity is null, that ways there should be no bend on the graph over that time interval. In other words, the bend is now straight on height of the 10-axis.
Finally, the daughter started picking upwardly speed, backtracking homeward. Hither the velocity graph gets interesting.
Assuming she had a abiding dispatch – that is, each 2d she was increasing her velocity by the same corporeality equally the second before – this ways her velocity was increasing at a constant rate. The twist in this scenario is that she also changed management.
Tips
-
Recall, a negative velocity does not mean slowing down (that's negative acceleration). It ways moving in the negative direction!
Altogether, that means the velocity-time graph for the last segment of her ride (t = 8 to t = 15) needs to testify a straight line where her velocity is growing negatively. In other words, a straight line moving from the x-axis at t = viii seconds in a diagonal towards the bottom right of the graph.
Acceleration-Time Graphs
These are often tricky for students; just call up the meaning of dispatch: a alter in velocity.
For the first eight seconds of her ride, the girl's velocity was non changing. (Again, ignoring her instantaneous shift from 2 m/s to stopped.)
That means for the first eight seconds her acceleration was zero.
Making the motion graph for this, where the y-axis is at present showing acceleration in 1000/stwo, is therefore pretty simple:
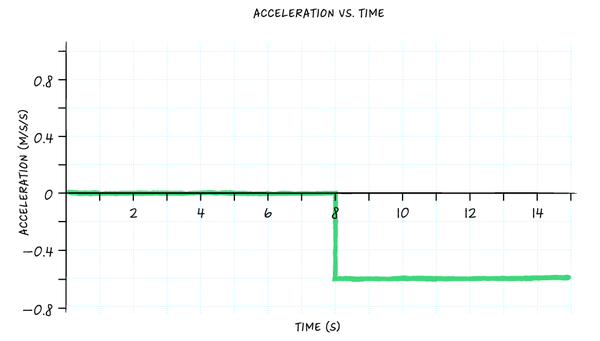
••• Dana Chen | Sciencing
Now, for the last portion of her ride, recall that her velocity was increasing at a constant rate in the negative direction. Since increasing velocity is acceleration, the acceleration-time graph should have a apartment line in the negative quadrant from viii seconds onward.
More Realistic Motion Maps
In the real world, acceleration is frequently not abiding. On the acceleration-time graph, this would look similar a curved line.
Calculating the corresponding position-time and velocity-time graphs to go with this is typically beyond the scope of a not-calculus-based physics form. Students are expected to realize a curved line is not constant, however, and that the graph indicates a irresolute dispatch.
Tips
-
Exam yourself: How would you revise each of the previous graphs (position-fourth dimension, velocity-fourth dimension and acceleration-time) to more than realistically bear witness the daughter's bike slowing down before her break? Try it before reading on!
The graph for position should wait roughly like to what information technology did before, but with any precipitous corners smoothed out. The aforementioned would happen with the velocity graph - rough corners become smoothed out. But in addition, the instantaneous jump on the velocity graph from ii m/s to 0 yard/s becomes a smooth, slanted line with a large negative slope instead of a vertical line.
On the dispatch graph, at around the five second marking, a steep bend would dip into the negative region before coming back to 0 to signal the negative acceleration required to come to a finish. And the jump that occurs at the viii second mark, instead of being vertical, would simply curve into a line with a large negative slope that then smoothly flattens out at -0.5 m/s/southward.
Source: https://sciencing.com/motion-graphs-position-velocity-acceleration-w-diagram-13720230.html
Posted by: mannsdockly.blogspot.com


0 Response to "How To Draw Acceleration Time Graph From Velocity Time Graph"
Post a Comment